Dalam menghadapi UNBK Matematika, kecepatan dan keakuratan dalam menjawab soal merupakan salah satu kunci biar waktu yang tersedia sanggup dipakai secara maksimal mungkin. Untuk itu dalam latihan ini, anda akan diperkenalkan banyak sekali model soal perihal peluang baik itu permutasi maupun kombinasi. Sehingga nantinya sehabis memahami baik model-model soal dibawah ini, anda akan dengan gampang sanggup memecahkan duduk kasus yang berkenaan dengan peluang.
Bagi anda yang membutuhkan pemahaman konsep teori yang disertai juga dengan pola soal perihal peluang, kombinasi dan permutasi, anda sanggup mengunjungi :
Contoh Soal Peluang Beserta Kunci Jawabannya
Contoh Soal Permutasi Dan Pembahasannya
Pengertian Kombinasi,Contoh Soal Dan Pembahasannya
Latihan Soal Matematika UNBK Peluang
Soal No.1 (UN 2002)Pada sebuah bidang datar terdapat 15 titik yang berbeda. Melalui setiap dua titik yang berbeda dibuat sebuah garis lurus. Jumlah garis lurus yang sanggup dibuat yaitu ...
A. 210
B. 105
C. 90
D. 75
E. 65
Pembahasan
Soal di atas kita jawab dengan memakai
Mengapa demikian ?
Perhatikan kata-kata : setiap dua titik yang berbeda dibuat sebuah garis lurus.Artinya kita hanya sanggup menciptakan garis melalui dua titik yang dihentikan sama.
C(15,2) =
C(15,2) =
C(15,2) =
Jawab : B
Kombinasi.Mengapa demikian ?
Perhatikan kata-kata : setiap dua titik yang berbeda dibuat sebuah garis lurus.Artinya kita hanya sanggup menciptakan garis melalui dua titik yang dihentikan sama.
C(15,2) =
15! / (15 - 2)! . 2!
C(15,2) =
15.14.13! / 13! . 2.1
C(15,2) =
210 / 2
= 105Jawab : B
Soal No.2 (UN 2003)
Jika sebuah dadu dan sekeping mata uang dilempar undi satu kali bersama, maka peluang untuk memperoleh gambar pada mata uang dan bilangan ganjil pada dadu yaitu ...
A.
1 / 12
B.
1 / 6
C.
1 / 4
D.
1 / 3
E.
1 / 2
Pembahasan
Mata uang mempunyai dua sisi yaitu : Angka (A) dan Gambar (G)
Dadu mempunyai enam sisi yang terdiri dari : 1, 2, 3, 4, 5, 6
Ruang sampel untuk mata uang dan dadu dilempar secara bersamaan :
Ruang Sampel (S) : {(A,1),(A,2),(A,3),(A,4),(A,5),(A,6), (G,1),(G,2),(G,3),(G,4),(G,5),(G,6)}
Dengan demikian diperoleh banyaknya anggota/ruang sampel : n(S) = 12
Titik sampel yang muncul gambar dan bilangan ganjil yaitu : (G,1), (G,3), (G,5)
Peluang untuk memperoleh gambar dan bilangan ganjil :
P =
Jawab : C
Dadu mempunyai enam sisi yang terdiri dari : 1, 2, 3, 4, 5, 6
Ruang sampel untuk mata uang dan dadu dilempar secara bersamaan :
Ruang Sampel (S) : {(A,1),(A,2),(A,3),(A,4),(A,5),(A,6), (G,1),(G,2),(G,3),(G,4),(G,5),(G,6)}
Dengan demikian diperoleh banyaknya anggota/ruang sampel : n(S) = 12
Titik sampel yang muncul gambar dan bilangan ganjil yaitu : (G,1), (G,3), (G,5)
Peluang untuk memperoleh gambar dan bilangan ganjil :
P =
3 / 12
= 1 / 4
Jawab : C
Soal No.3 (UN 2004)
Dua buah dadu dilambungkan bersama-sama. Peluang muncul mata dadu pertama 3 dan mata dadu kedua 5 yaitu ...?
A.
6 / 36
B.
5 / 36
C.
4 / 36
D.
3 / 36
E.
1 / 36
Pembahasan
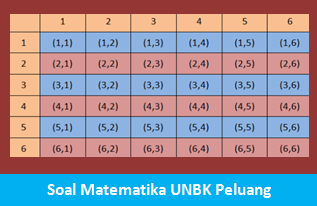
Dua buah dadu dilempar secara bersamaan akan menghasilkan sampel menyerupai gambar di bawah ini :
Ruang Sampel (S) : {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5), (4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.
Banyaknya ruang sampel , n(S) = 36
Peluang muncul mata dadu pertama 3 dan mata dadu kedua 5:
P =
Jawab : E
Banyaknya ruang sampel , n(S) = 36
Peluang muncul mata dadu pertama 3 dan mata dadu kedua 5:
P =
1 / 36
Jawab : E
Soal No.4 (UN 2005)
Sebuah kotak berisi 5 bola merah , 4 bola biru dan 3 bola kuning. Dari dalam kotak diambil 3 bola sekaligus secara acak. Peluang terambil 2 bola merah dan 1 bola biru yaitu ...
A.
1 / 10
B.
5 / 36
C.
1 / 6
D.
2 / 11
E.
4 / 11
Pembahasan
Cara mengambil 2 bola merah :
C(5,2) =
C(5,2) =
C(5,2) =
Cara mengambil 1 bola biru :
C(4,1) =
C(4,1) =
Pengambilan bola sekaligus :
C(12,3) =
C(12,3) =
C(12,3) =
Peluang terambilnya 2 bola merah dan 1 bola biru :
P =
P =
P =
Jawab : D
C(5,2) =
5! / (5-2)! . 2!
C(5,2) =
5.4.3! / 3! . 2.1
C(5,2) =
20 / 2
= 10 CaraCara mengambil 1 bola biru :
C(4,1) =
4! / (4-1)! . 1!
C(4,1) =
4 . 3! / 3! . 1
= 4 caraPengambilan bola sekaligus :
C(12,3) =
12! / (12-3)! . 3!
C(12,3) =
12.11.10.9! / 9! . 3.2.1
C(12,3) =
1320 / 6
= 220 caraPeluang terambilnya 2 bola merah dan 1 bola biru :
P =
C(5,2) . C(4,1) / C(12,3)
P =
10 . 4 / 220
P =
2 / 11
Jawab : D
Soal No.5 (UN 2006)
Di dalam sebuah kotak terdapat 10 butir telur, 4 diantaranya busuk. Jika diambil secara acak tiga butir sekaligus, maka peluang terambilnya 3 telur wangi adalah...
A.
3 / 120
B.
4 / 120
C.
12 / 120
D.
24 / 120
E.
48 / 120
Pembahasan
Misalkan A = {terambil telur busuk}
n(A) = C(4,3) =
n(S)= C(10,3) =
P(A) =
n(A) = C(4,3) =
4! / (4-3)! . 3!
= 4 n(S)= C(10,3) =
10! / (10-3)! . 3!
= 120 P(A) =
n(A) / n(S)
= 4 / 120
Soal No.6
Dari 10 butir telur terdapat 2 butir yang busuk. Seorang ibu membeli 2 butir telur tanpa memilih. Peluang menerima 2 butir telur yang baik yaitu ...
A.
9 / 45
B.
11 / 45
C.
14 / 45
D.
18 / 45
E.
28 / 45
Pembahasan
Terdapat 10 butir telur, alasannya yaitu wangi 2, berarti yang bagus hanya 8 buah
Banyaknya mengambil 2 butir telur dari 10 butir telur yaitu :
n(S) = C(10,2)
n(S) =
n(S) =
Banyaknya mengambil 2 telur yang bagus dari 8 telur yang baik yaitu :
n(A) = C(8,2)
n(A) =
n(A) =
P(A) =
Jawab : E
Banyaknya mengambil 2 butir telur dari 10 butir telur yaitu :
n(S) = C(10,2)
n(S) =
10! / (10-2)! . 2!
n(S) =
10.9.8! / 8! . 2.1
= 45 Banyaknya mengambil 2 telur yang bagus dari 8 telur yang baik yaitu :
n(A) = C(8,2)
n(A) =
8! / (8-2)! . 2!
n(A) =
8.7.6! / 6! . 2.1
= 28 P(A) =
n(A) / n(S)
= 28 / 45
Jawab : E
Soal No.7
Dalam suatu ruangan terdapat 25 orang, setiap orang saling bersalaman. Banyaknya salaman yang diakukan adalah....
A. 600
B. 400
C. 300
D. 150
E. 500
Pembahasan
Soal di atas kita jawab dengan memakai kombinasi
Banyaknya salaman = C(25,2)
Banyaknya salaman =
Banyaknya salaman =
Banyaknya salaman =
Jawab : C
Banyaknya salaman = C(25,2)
Banyaknya salaman =
25! / (25-2)! . 2!
Banyaknya salaman =
25.24.23! / 23! . 2.1
Banyaknya salaman =
600 / 2
= 300 Jawab : C
Soal No.8
10 orang finalis suatu lomba kecantikan akan dipilih secara acak 3 yang terbaik. Banyak cara pemilihan tersebut ada.....cara.
A. 70
B. 80
C. 120
D. 360
E. 720
Pembahasan
C(10,3) =
C(10,3) =
C(10,3) =
Jawab : C
10! / (10-3)! . 3!
C(10,3) =
10.9.8.7! / 7! . 3.2.1
C(10,3) =
720 / 6
= 120 cara Jawab : C
Soal No.9 (UN 2009)
Daru seperangkat kartu bridge diambil dua kartu sekaligus secara acak. Peluang yang terambil dua kartu king yaitu ...
A.
1 / 221
B.
1 / 13
C.
4 / 221
D.
11 / 221
E.
8 / 663
Pembahasan
Kartu Bridge terdiri dari 52 buah
Kartu King terdiri dari 4 buah
Banyaknya cara mengambil 2 kartu dari 52 kartu yaitu :
n(S) = C(52,2)
n(S) =
n(S) =
n(S) =
Banyaknya cara mengambil 2 kartu king dari 4 kartu king yang tersedia yaitu :
n(A) = C(4,2)
n(A) =
n(A) =
Peluang terambilnya dua kartu king yaitu :
P(A) =
P(A) =
Jawab :A
Kartu King terdiri dari 4 buah
Banyaknya cara mengambil 2 kartu dari 52 kartu yaitu :
n(S) = C(52,2)
n(S) =
52! / (52-2)! . 2!
n(S) =
52.51.50! / 50! . 2.1
n(S) =
52.51. / 2
= 1326Banyaknya cara mengambil 2 kartu king dari 4 kartu king yang tersedia yaitu :
n(A) = C(4,2)
n(A) =
4! / (4-2)! . 2!
n(A) =
4.3.2! / 2! . 2.1
= 6 Peluang terambilnya dua kartu king yaitu :
P(A) =
n(A) / n(S)
P(A) =
6 / 1326
= 1 / 221
Jawab :A
Soal No.10 (UN 2015)
Dalam suatu organisasi akan dipilih pengurus sebagai ketua, sekretaris dan bendahara dari 12 calon yang memenuhi kriteria. Banyak susunan pengurus yang mungkin dari 12 calon tersebut yaitu ...
A. 27
B. 36
C. 220
D. 1.320
E. 2.640
Pembahasan
Karena susunan memperhatikan urutan, maka kita gunakan Permutasi :
P(12,3) =
P(12,3) =
Jawab : D
P(12,3) =
12! / (12-3)!
P(12,3) =
12.11.10.9! / 9!
= 1320Jawab : D
Soal No.11 (UN 2015)
Dari 11 orang calon Kapolda akan dipilih 4 orang sebagai Kapolda untuk ditempatkan di empat provinsi, banyak cara pemilihan yang mungkin yaitu ...
A. 44
B. 256
C. 330
D. 7.920
E. 10.000
Pembahasan
Karena susunan memperhatikan urutan, maka kita gunakan Permutasi :
P(11,4) =
P(11,4) =
Jawab : D
P(11,4) =
11! / (11-4)!
P(11,4) =
11.10.9.8.7! / 7!
= 7920Jawab : D
Soal No.12
Banyak bilangan yang terdiri atas 3 angka yang disusun dari angka 1, 2, 3, 4, 5, 6, 7 dan 8 yaitu ....
A. 44
B. 336
C. 330
D. 234
E. 122
Pembahasan
Karena susunan memperhatikan urutan, maka kita gunakan Permutasi :
P(8,3) =
P(8,3) =
Jawab : B
P(8,3) =
8! / (8-3)!
P(8,3) =
8.7.6.5! / 5!
= 336Jawab : B
Soal No.13
Banyaknya susunan berbeda yang sanggup dibuat dari aksara ‘ALAMATMU’ yaitu ....
A. 3360
B. 3365
C. 1330
D. 2134
E. 1122
Pembahasan
Permutasi unsur sama dimana A = 3 dan M = 2
Maka, banyak susunan berbeda =
Jawab : A
Maka, banyak susunan berbeda =
8! / 2!.3!
= 8.7.5.4.3=3360 Jawab : A
Soal No.14 (UN 2016)
Dalam sebuah ujian terdapat 10 soal, dari nomor 1 hingga nomor 10. Peserta ujian wajib mengerjakan soal 1, 3 dan 5 serta hanya mengerjakan 8 dari 10 soal yang tersedia. Banyak cara penerima ujian menentukan soal yang dikerjakan yaitu ...
A. 21
B. 28
C. 45
D. 48
E. 56
Pembahasan
Karena susunan memperhatikan urutan, maka kita gunakan Permutasi :
Banyak cara siswa mengerjakan 8 dari 10 soal yang tersedia dengan syarat 3 buah soal tertentu wajib dikerjakan yaitu :
C(7,5) =
C(7,5) =
Jawab : A
Banyak cara siswa mengerjakan 8 dari 10 soal yang tersedia dengan syarat 3 buah soal tertentu wajib dikerjakan yaitu :
C(7,5) =
7! / (7-5)! . 5!
C(7,5) =
7.6.5! / 2! . 5!
= 21Jawab : A
Soal No.15 (UN 2017)
Diberikan 5 aksara konsonan c, k, m, r, dan s serta 3 aksara vokal a, i, dan u. Dari aksara tersebut akan dibuat sebuah password yang terdiri atas 5 aksara dengan 3 aksara konsonan dan 2 aksara vokal berbeda. Banyak password yang terbentuk yaitu ...
A. 1.400
B. 2.500
C. 3.600
D. 4.700
E. 5.800
Pembahasan
Banyak cara menentukan 3 dari 5 aksara konsonan :
C(5,3) =
Banyak cara menentukan 2 dari 3 aksara vokal :
C(3,2) =
Banyak susunan 3 aksara konsonan dan 2 aksara vokal :
5! = 120
Maka , banyak password yang yang terbentuk yaitu :
10 × 3 × 120 = 3.600
Jawab : C
C(5,3) =
5! / (5-3)! . 3!
= 10Banyak cara menentukan 2 dari 3 aksara vokal :
C(3,2) =
3! / (3-2)! . 2!
= 3Banyak susunan 3 aksara konsonan dan 2 aksara vokal :
5! = 120
Maka , banyak password yang yang terbentuk yaitu :
10 × 3 × 120 = 3.600
Jawab : C
Advertisement